Навигационная цепочка "где я сейчас?" - траектория от главной до текущей страницы сайта. Breadcrumbs.
Передовица (меню разделов)
⇓
Документы
⇓
ИиО
⇓
Единый методический подход к задачам на построение сложных компьютерных изображений
Единый методический подход к задачам на построение сложных компьютерных изображений (N1/1993)
М.Степанов. Группа сайта просит вас связаться с нами! (ЗАЧЕМ ЭТО?)
В курсе информатики, как правило, рассматриваются задачи на построение довольно простых компьютерных изображений, например, таких как эллипс с осями, параллельными сторонам экрана, и графики элементарных функций. Однако, достаточно естественное обобщение этих задач может вызвать значительные затруднения у самых сильных учащихся. В случае эллипса таким обобщением является задача на построение наклонного эллипса, а в случае графика - задачи на построение изображений пространственных кривых и поверхностей. Но даже решив одну из этих задач, учащийся не получает метода решения другой.
В данной статье предлагается единый методический подход к решению подобных задач, который разработан автором в рамках факультативного курса математического моделирования и является одним из фрагментов общей методики курса. Основная идея, обеспечивающая единство подхода, состоит в том, что геометрические формы трактуются как следы движущегося объекта. При этом все необходимые математические понятия вводятся неформально с опорой на моторную интуицию учащегося, что делает их вполне доступными. На основе приводимых ниже заданий можно вести самостоятельный факультативный курс. Для преподавателя полезно знакомство с работой [1].
Изложение ведётся применительно к версии языка Бейсик, реализованной на ПЭВМ "Агат", но программы легко могут быть перенесены на другие компьютеры, предоставляющие доступ к графике. Задачи группируются в разделы, каждый из которых посвящён новым приёмам построения изображений. В некоторых программах используются одни и те же подпрограммы, поэтому каждая такая подпрограмма получает имя и размещается в строках программы с фиксированными номерами.
1. Подготовительный этап. Параметрическое задание линий
Задание 1.1. Напишите программу, осуществляющую движение точки по экрану. При этом каждый раз точка должна смещаться вдоль осей X и Y на фиксированные расстояния DX и DY (рис.1). Какова траектория точки?
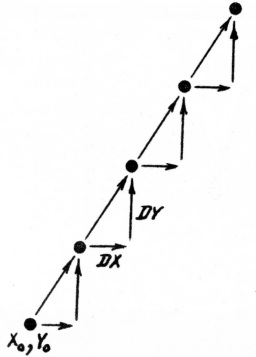
Решение. Легко понять, что точка движется по прямой. Если DX и DY превосходят 1, то след точки является пунктиром.
10 HGR=1: COLOR=15: REM ВКЛЮЧЕНИЕ ГРАФ.РЕЖ. 20 X0=30: Y0=40 30 DX=5: DY=4 40 N=40: REM КОЛИЧЕСТВО СКАЧКОВ 50 FOR T=0 TO N 60 PLOT X0+T*DX, Y0+T*DY: REM УСТАНОВКА ТОЧКИ 70 NEXT T 80 GET F¤: TEXT=0: END: REM ЗАДЕРЖКА ДО НАЖАТИЯ
Величина T из задания 1.1 может рассматриваться не только как номер очередной точки, но и как время, а величины DX и DY как горизонтальная и вертикальная составляющие скорости точки. Вычисление координаты этой точки производится по формулам:
X=X0+T*DX (1) Y=Y0+T*DY
Задание 1.2. Напишите программу для проведения отрезков, концы которых могут лежать вне экрана.
Решение. Величина T в формулах (1) подобно физическому времени может принимать любые действительные значения, а не только натуральные. Предположим, что точка из положения (X0, Y0) должна за единицу времени перейти в положение (X1, Y1). Общее смещение точки по оси X при этом переходе равно DX=Y1-Y0. Легко проверить, что при T=0 и T=1 формула (1) даёт нужные начальные и конечные координаты, а при промежуточных значениях T - координаты промежуточных точек отрезка.
Поскольку в программе переменная T не может быть непрерывной, необходимо выбрать шаг, с которым будет меняться эта переменная. При этом следует исходить из того, что отрезок должен быть сплошным, а значит и его проекции на вертикаль и горизонталь тоже должны быть сплошными (рис.2). Количество точек отрезка равно наибольшему из модулей чисел DX и DY. Прежде чем применить оператор установки точки, следует проверить, попала ли она в экран.
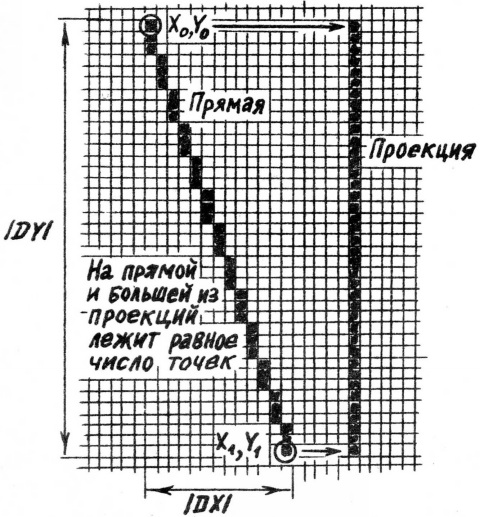
10 HGR=1: COLOR=15 20 X0=10: Y0=-10 30 X1=265: Y1=265 40 GOSUB 2000 50 GET F¤: TEXT=0: END 2000 REM ОТРЕЗОК 2005 REM ВХОД.ВЕЛ. X0,Y0,X1,Y1 2010 REM ПРОЧИЕ ВЕЛ. XN,YN,XK,YK,DX,DY,NN,T,XT,YT 2015 XN=INT(X0): YN=INT(Y0) 2020 XK=INT(X1): YK=INT(Y1) 2025 DX=XK-XN: DY=YK-YN 2030 GOSUB 4000 2035 IF NN=0 THEN GOSUB 3000: RETURN 2040 FOR T=0 TO 1 STEP 1/NN 2045 XT=XN+T*DX: YT=YN+T*DY 2050 GOSUB 3000 2055 NEXT T 2060 RETURN 2065 REM КОНЕЦ 3000 REM ОБРАБОТКА КООРД. 3010 IF XT=>0 AND XT=<255 OR YT=>0 OR YT=<255 THEN PLOT XT,YT 3020 RETURN 4000 REM ВЫБОР ШАГА 4010 NN=ABS(DX) 4020 IF NN<ABS(DY) THEN NN=ABS(DY) 4030 RETURN
Задание 1.3. Самостоятельно напишите программу для проведения отрезка-пунктира с заданным шагом.
Задание 1.4. Расчертите экран параллельными наклонными прямыми (рис.3).
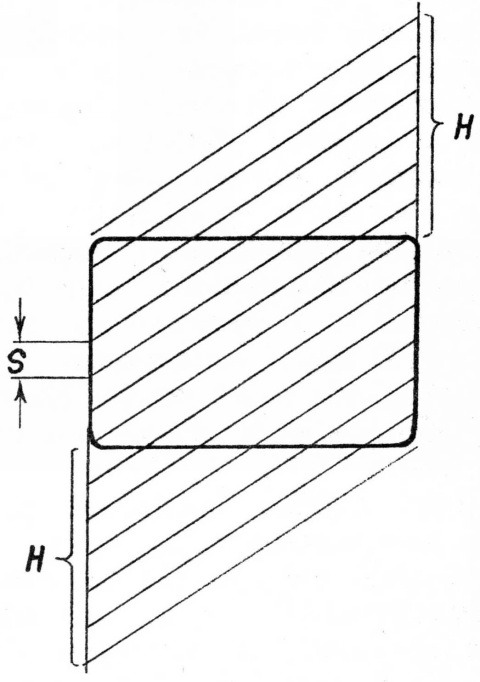
Решение.
10 HGR=1: COLOR=15 20 X0=0: X1=255: H=145: S=20 30 FOR Y0=0 TO 255+H STEP S 40 Y1=Y0-H 50 GOSUB 2000 60 NEXT Y0 70 GET F¤: TEXT=0: END 2000 REM ОТРЕЗОК ...............................
В задании 1.2 из формул (1) получены новые формулы, с помощью которых единичный отрезок отображается на произвольный отрезок с концами (X0, Y0) и (X1, Y1).
X=X0+T*(X1-X0) (2) Y=Y0+T*(Y1-Y0)
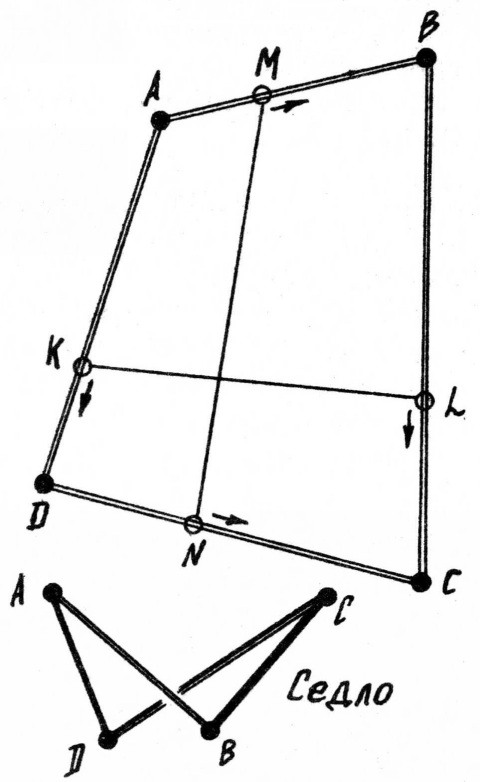
Задание 1.5. На экране задан четырёхугольник ABCD. По его сторонам равномерно движутся 4 точки, каждая из которых проходит сторону за единицу времени. Точки M и N, K и L соединены резиновыми жгутами (рис.4). Начертите на экране следы этих жгутов, оставляемые через равные промежутки времени.
Решение. Сначала построим следы, оставляемые жгутом MN, а затем аналогичным способом - следы от жгута KL. Для одного и того же значения величины T по формулам (2) вычислим координаты точек M и N, а затем соединим эти точки отрезком.
10 HGR=1: COLOR=15 20 DATA 10,10,160,170,240,0,80,190 30 N=16: REM КОЛ-ВО СЛЕДОВ ЖГУТА 40 READ XA,YA,XB,YB,XC,YC,XD,YD 50 FOR T=0 TO 1 STEP 1/N 60 X1=XA+T*(XB-XA): Y1=YA+T*(YB-YA) 70 X2=XD+T*(XC-XD): Y2=YD+T*(YC-YD) 80 PLOT X1,Y1 TO X2,Y2: REM ПРОВЕДЕНИЕ ОТРЕЗКА 90 NEXT T 100 FOR T=0 TO 1 STEP 1/N 110 X1=XA+T*(XD-XA): Y1=YA+T*(YD-YA) 120 X2=XB+T*(XC-XB): Y2=YB+T*(YC-YB) 130 PLOT X1,Y1 TO X2,Y2 140 NEXT T 150 GET F¤: TEXT=0: END
При различном расположении вершин четырёхугольника на экране может быть получено изображение седла или перекошенной решётки.
Для построения отрезка мы использовали формулы (2), в которых координаты точки, движущейся по отрезку, зависят от одной величины, называемой параметром. В формулах (2) зависимость является линейной. Если же использовать другие функциональные зависимости координат движущейся точки от параметра, можно получить вместо отрезков различные виды кривых. Параметр при этом можно воспринимать не только как время, но как величину, имеющую геометрический смысл.
Задание 1.6. Получите формулы для параметрического представления окружности и постройте окружность на экране.
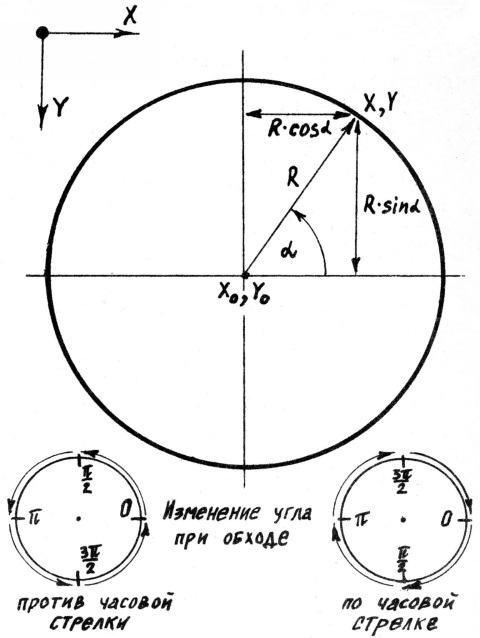
Решение. Окружность на плоскости задаётся координатами центра и радиусом, поэтому эти величины являются исходными. На роль параметра удобнее всего взять центральный угол. На рис.5 легко усмотреть формулы
X=X0+R*cos α (3) Y=Y0-R*sin α
В языке Бейсик аргумент тригонометрических функций задаётся в радианах, поэтому мы будем использовать только радианную меру. При выводе формул (3) предполагалось, что угол растёт при обходе окружности против часовой стрелки. Чтобы изменить направление обхода, достаточно изменить знак перед членом R*sin α.
Поскольку экранные точки на "Агате" имеют форму прямоугольничков, а не квадратиков, то окружность на экране примет форму эллипса. Для корректировки изображения следует ввести коэффициент сжатия K. Подробнее об этом говорится в следующем задании.
10 HGR=1: COLOR=15: PI=4*ATN(1) 20 X0=128: Y0=128: R=120: K=1 30 A0=0: A1=2*PI 40 GOSUB 2100 50 GET F¤: TEXT=0: END 2100 REM ЭЛЛИПС 2105 REM ВХОД.ВЕЛ. X0,Y0,R,A0,A1,K 2110 REM ПРОЧИЕ ВЕЛ. UG,DU,XT,YT 2115 GOSUB 4100 2120 FOR UG=A0 TO A1+.1 STEP DU 2125 XT=X0+R*COS(UG) 2130 YT=Y0-K*R*SIN(UG) 2135 GOSUB 3100 2140 NEXT UG 2145 RETURN 2150 REM КОНЕЦ 3100 REM ОБРАБ.КООРД. 3110 IF UG=A0 THEN PLOT XT,YT 3120 IF UG<>A0 THEN PLOT TO XT, YT: REM ОТРЕЗОК ОТ ПОСЛЕДНЕЙ ПОСТАВЛЕННОЙ РАНЕЕ ТОЧКИ 3130 RETURN 4100 REM ВЫБОР ШАГА 4110 DU=PI/18 4120 RETURN
Задание 1.7. Исходя из того, что эллипс является сжатой (или растянутой) окружностью (рис.6), выведите формулу для параметрического представления сжатого (растянутого) по вертикали эллипса. Подберите коэффициент сжатия так, чтобы эллипс на экране выглядел окружностью.
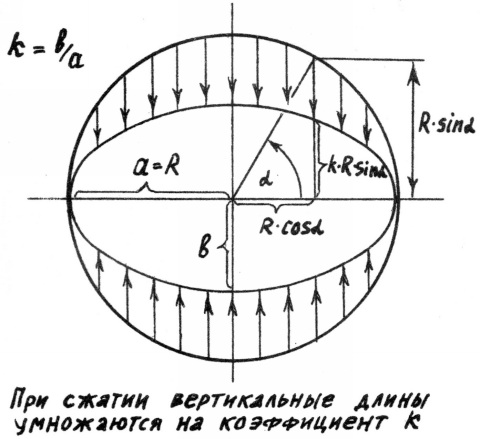
Решение. Окружность задаётся формулами (3). Из рис.6 видно, что при вертикальном сжатии координата X не изменяется, а вертикальный отрезок длины R*sin α становится равным K*R*sin α. Отсюда получаем параметрическое задание эллипса
X=X0+R*cos α=X0+A*cos α y=Y0-K*R*sin α=Y0-B*sin α (4)
Формула соответствует программе "Эллипс" из задания 1.6. При K>0 построение эллипса производится против часовой стрелки, а при K<0 - по часовой. Для выбора значения коэффициента K, позволяющего получить окружность, используем программу
10 HGR=1: COLOR=15: PI=4*ATN(1) 20 X0=128: Y0=128: R=50 30 A0=0: A1=2*PI 40 FOR K=1/3 TO 5/3 STEP 1/6 50 GOSUB 2100 60 NEXT K 70 GET F¤: TEXT=0: END 2100 REM ЭЛЛИПС .............................
В результате получаем, что искомое значение K равно 5/3.
Задание 1.8. Разберитесь, как построить дугу окружности или эллипса.
Решение. Чтобы задать дугу, необходимо указать на эллипсе две точки, начальную и конечную, и выбрать направление обхода. Концы дуги мы будем задавать углами α0 и α1 (что уже учтено в подпрограмме "Эллипс"), а направление обхода - знаком коэффициента сжатия.
При организации цикла угол должен возрастать от α0 до α1, однако, в тех случаях, когда внутрь дуги попадает точка, задаваемая нулевым углом (рис.7), может оказаться, что α1<α0. Чтобы исправить положение, нужно заменить угол α1 на угол α1+2π, при этом предполагается, что исходные значения углов α0 и α1 заключены между 0 и 2*π. В дальнейшем мы будем использовать подпрограмму "Эллипс" и для углов, выходящих за эти границы. При этом дуга может быть несколько раз закручена вокруг эллипса, например, при α0=0 и α1=10π дуга делает 5 оборотов. В таких случаях мы будем следить за тем, чтобы α0 было меньше α1.
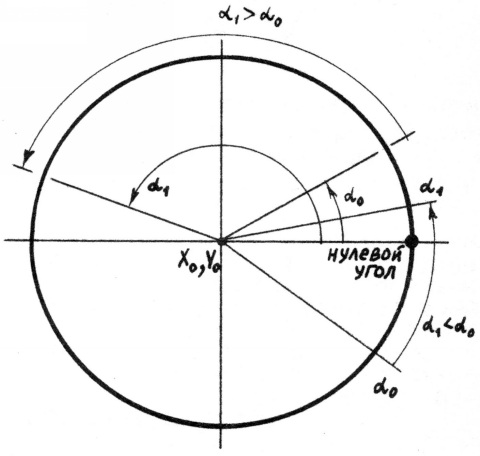
Выбор шага производится без учёта радиуса, что неоправданно замедляет работу программы для маленьких окружностей. Попытайтесь усовершенствовать подпрограмму "Выбор шага".
10 HGR=1: COLOR=15: PI=4*ATN(1) 20 X0=128: Y0=128: R=50 30 A0=3*PI/2: A1=PI/2 40 FOR K=0 TO -5/3 STEP -1/3 50 GOSUB 2100 60 NEXT K 70 GET F¤: TEXT=0: END 2100 REM ЭЛЛИПС ..................................... 3100 REM ОБРAБ.КООРД. ..................................... 4100 REM ВЫБОР ШАГА 4110 IF A1<A0 THEN A1=A1+2*PI 4120 NN=INT((A1-A0)*18/PI)+1 4130 DU=(A1-A0)/NN 4140 RETURN
Нами получены параметрические представления отрезка, окружности и эллипса. Используя другие функциональные зависимости координат X и Y от параметра, можно получить представления различных кривых. В частности, график функции y=f(x) может быть задан параметрически
x=t y=f(t)
Существует и ещё один способ параметрического задания кривых - составление кривой из дуг окружностей и прямолинейных отрезков. Кривая складывается из кусков, каждый из которых имеет свою параметризацию. Подобное задание кривой назовём кусочной параметризацией.
Задание 1.9. С помощью кусочной параметризации постройте сердечко.
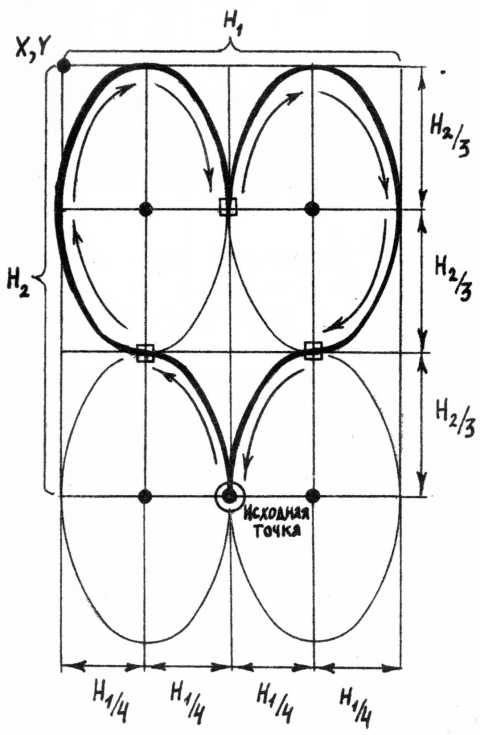
Решение. На рис.8 представлено разбиение сердечка на 4 дуги равных между собой эллипсов. У всех эллипсов полуоси равны H1/4 и H2/3. Точно так же, в долях H1 и H2, будем выражать координаты их центров. Углы будем выражать в долях π. Направление обхода дуги зададим с помощью величины SK, равной либо +1, либо -1.
10 HGR=1: COLOR=15: PI=4*ATN(1) 20 X=5: Y=5: H1=245: H2=245 30 R=H1/4: KK=(H2/3)/(H1/4) 40 DATA .25,1,0,.5,1 50 DATA .25,.33,.5,2,-1 60 DATA .75,.33, 1,.5,-1 70 DATA .75,1,.5,1,1 B0 FOR I=1 TO 4 90 READ DX,DY,A0,A1,SK 100 X0=X+DX*H1: Y0=Y+DY*H2 110 A0=PI*A0: A1=PI*A1 120 K=KK*SK 130 GOSUB 2100 140 NEXT I 150 GET F¤: TEXT=0: END 2100 REM ЭЛЛИПС ...........................
Задание 1.10. Постройте сложное изображение, состоящее из дуг и отрезков (рис.9).
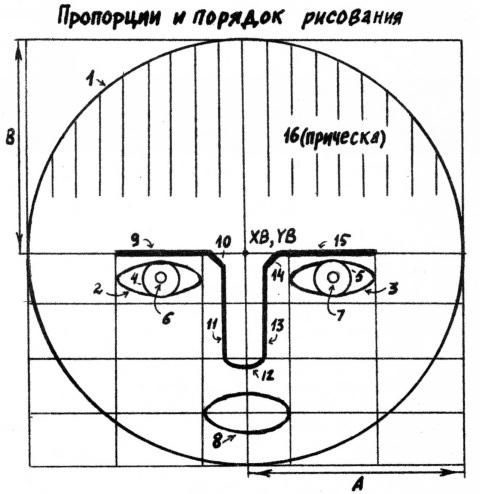
Решение. Основной проблемой является унификация обращения к подпрограммам. Мы решаем её следующим образом. Для каждого элемента изображения буквой русского алфавита указывается его тип (Э - эллипс, П - прямолинейный отрезок, Д - дуга). В зависимости от типа специальными подпрограммами производится считывание информации и её преобразование, после чего используется подпрограмма построения соответствующего элемента.
Буквой "С" помечаются специализированные подпрограммы, которые связаны с особенностями именно этого изображения. В нашем случае используется специализированная подпрограмма построения причёски.
Может показаться, что использование подпрограммы "Отрезок" только замедляет работу программы, ведь прямые можно сразу провести оператором PLOT. Однако в дальнейшем мы воспользуемся тем, что в подпрограммах "Отрезок" и "Эллипс" можно перехватывать промежуточные координаты и преобразовывать их.
10 HGR=1: COLOR=15: PI=4*ATN(1): KE=16 20 XB=128: YB=96: A=64: B=80 30 DATA "Э",0,0,1,1.25 40 DATA "Э",-.4,.09,.2,.08 50 DATA "Э",.4,.09,.2,.08 60 DATA "Э",4,.09,.08,.08 70 DATA "Э",.4,.09,.08,.08 80 DATA "Э",-.4,.09,.04,.04 90 DATA "Э",.4,.09,.04,.04 100 DATA "Э",0,.67,.2,.08 110 DATA "П",-.6,0,-.14,0 120 DATA "П",-.14,0,-.07,.058 130 DATA "П",-.07,.058,-.07,.5 140 DATA "Д",0,.5,.07,.02,1,2 150 DATA "П",.07,.5,.07,.058 160 DATA "П",.07,.058,.14,.0 170 DATA "П",.14,0,.6,0 180 DATA "С" 190 FOR I=1 TO KE 200 READ PR¤ 210 IF PR¤="П" THEN GOSUB 1000 220 IF PR¤="Э" THEN GOSUB 1100 230 IF PR¤<"Д" THEN GOSUB 1200 240 IF PR<="C" THEN GOSUB 1300 250 NEXT I 260 GET F¤: TEXT=0: END 1000 REM П 1010 READ X0,Y0,X1,Y1 1020 X0=XB+X0*A: Y0=YB+Y0*B 1030 X1=XB+X1*A: Y1=YB+Y1*B 1040 GOSUB 2000 1050 RETURN 1100 REM Э 1110 READ X0,Y0,AA,BB 1120 X0=XB+X0*A: Y0=YB+Y0*B 1130 R=AA*A: K=BB/AA: A0=0: A1=2*PI 1140 GOSUB 2100 1150 RETURN 1200 REM Д 1210 READ X0,Y0,AA,BB,A0,A1 1220 X0=XB+X0*A: Y0=YB+Y0*B 1230 R=AA*A: K=BB/AA 1240 A0=A0*PI: A1=A1*PI 1250 GOSUB 2100 1260 RETURN 1300 REM С 1310 Y1=YB-B*SIN(PI/18) 1320 FOR AL=PI/9 TO 8*PI/9 STEP PI/18 1330 X0=XB+A*COS(AL): Y0=YB-B*SIN(AL) 1340 X1=X0 1350 GOSUB 2000 1360 NEXT AL 1370 RETURN 2000 REM ОТРЕЗОК ..................................... 2100 REM ЭЛЛИПС .....................................
2. Эллипс и построение объёмных изображений
Если вращать твёрдое тело вокруг некоторой оси с тем, чтобы выбрать подходящий ракурс, любая его точка будет описывать круговую траекторию. Иногда по одной окружности могут двигаться сразу несколько важных для формы тела точек (например, вершин многогранника). Часто удобно строить изображение тела на плоскости, отправляясь именно от этих круговых траекторий. Поскольку окружность, как правило, кажется наблюдателю эллипсом, эллипс и его параметрическое представление приобретают важную роль при построении объёмных изображений.
Задание 2.1. Постройте изображение прямого кругового цилиндра. Можно ли аналогичным способом построить изображения наклонного цилиндра и конуса?
Решение. Изменим подпрограмму обработки координат эллипса.
10 HGR=1: COLOR=15: PI=4*ATN(1) 20 X0=128: Y0=50: R=100: K=.5: H=90 30 A0=0: A1=2*PI 40 GOSUB 2100 50 GET F¤: TEXT=0: END 2100 REM ЭЛЛИПС ..................................... 3100 REM ОБРАБОТКА КООРДИНАТ ЭЛЛИПСА 3110 IF UG=A0 THEN XP=XT: YP=YT 3120 IF UG=A0 THEN PLOT XT,YT TO XT,YT+H: RETURN 3130 IF ABS(UG-PI)<.01 THEN PLOT XT,YT TO XT,YT+H 3140 PLOT XT,YT TO XP,YP 3150 IF UG<PI THEN PLOT XT,YT+H TO XP,YP+H 3160 XP=XT: YP=YT 3170 RETURN 4100 REM ВЫБОР ШАГА 4110 DU=PI/18: RETURN
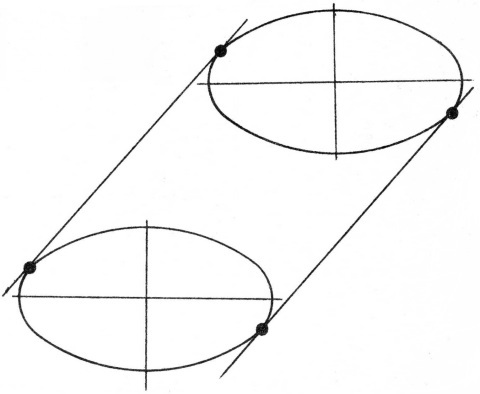
Построить наклонный цилиндр и конус без дефектов мы пока не можем, так как не умеем проводить касательных к эллипсу (рис.10).
Задание 2.2. Для того чтобы придать рисунку большую выразительность, элементы изображения закрашивают. Закрасьте верхнее основание цилиндра, не прибегая к помощи специального оператора закраски, даже если он реализован на вашем компьютере.
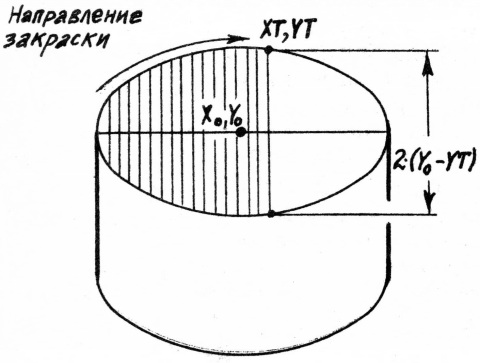
Решение. Будем закрашивать эллипс вертикальными прямыми (рис.11). Для этого введём в программу из задания 2.1 подпрограмму "Отрезок" с изменённой подпрограммой обработки координат отрезка. Изменим и дополним подпрограмму обработки координат эллипса со строки 3140.
3000 REM ОБРАБОТКА КООРДИНАТ ОТРЕЗКА 3010 PLOT XT,YT TO XT,YT+2*(Y0-YT) 3020 RETURN ..................................... 3140 IF UG<PI THEN PLOT XT,YT TO XP,YP 3150 IF UG<PI THEN PLOT XT,YT+H TO XP,YP+H 3160 IF UG<=PI THEN XP=XT: YP=YT: RETURN 3165 X0=XP: Y0=YP 3170 X1=XT: Yl=YT 3175 GOSUB 2000 3180 XP=Xl: YP=Yl 3185 RETURN
Задание 2.3. Постройте изображение правильного n-угольника, вписанного в окружность.
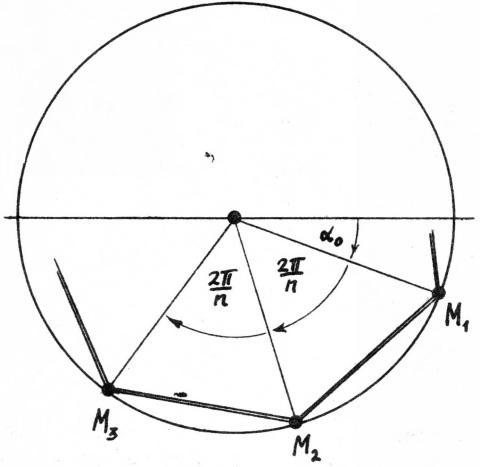
Решение. Построение правильного n-угольника ничем кроме шага, с которым меняется угол, не отличается от построения окружности или эллипса. В случае эллипса сжат будет и многоугольник.
10 HGR=1: COLOR=15: PI=4*ATN(1) 20 X0+128: Y0=128: R=72: K=-5/3 30 A0=PI/16: A1=A0+2*PI: N=5 40 GOSUB 2100 50 GET F¤: TEXT=0: END 2100 REM ЭЛЛИПС ..................................... 3100 REM ОБРАБОТКА КООРДИНАТ ЭЛЛИПСА 3110 IF UG=A0 THEN PLOT XT,YT 3120 IF UG<>A0 THEN PLOT TO XT,YT 3130 RETURN 4100 REM ВЫБОР ШАГА 4110 DU=2*PI/NI: RETURN
Задание 2.4. Постройте изображение усечённой пирамиды.
Решение. На экране будем строить все рёбра пирамиды, в том числе и невидимые. Вершины пирамиды лежат на двух эллипсах, поэтому основания могут быть построены по образцу задания 2.3.
Поскольку при соединении вершин многогранников могут возникнуть определённые сложности, начиная с этого задания мы будем сначала вычислять координаты всех вершин, сохраняя их в массивах, а затем соединять их рёбрами.
10 HOME: PRINT "СЧЕТ": REM ОЧИСТКА ЭКРАНА 20 N=5: DIM XH(N),YH(N),XL(N),YL(N) 30 NM=0: REM ИНДЕКС МАССИВА 40 DATA 150,50,50 50 DATA 105,150,100 60 PI=4*ATN(1): A0=PI/6: Al=A0+2*PI: K=-.5 70 FOR I=1 TO 2 80 READ X0,Y0,R 90 GOSUB 2100 100 NEXT I 110 HGR=1: COLOR=15 120 GOSUB 5000 130 GET F¤: TEXT=0: END 2100 REM ЭЛЛИПС ..................................... 3100 REM ОБРАБОТКА КООРДИНАТ ЭЛЛИПСА 3110 IF I=1 THEN XH(NM)=XT: YH(NM)=YT 3120 IF I=2 THEN XL(NM)=XT: YL(NM)=YT 3130 NM=NM+l: IF NM>N THEN NM=0 3140 RETURN 4100 REM ВЫБОР ШАГА 4110 DU=2*PI/N: RETURN 5000 REM ПИРАМИДА 5010 FOR NM=0 TO N-1 5020 PLOT XH(NM),YH(NM) TO XH(NM+1),YH(NM+1) 5030 PLOT XL(NM),YL(NM) TO XL(NM+1),YL(NM+1) 5040 PLOT XH(NM),YH(NM) TO XL(NM),YL(NM) 5050 NEXT NM 5060 RETURN
Задание 2.5. Удалите из изображения пирамиды невидимые рёбра.
Решение. Мы не можем сколько-нибудь подробно обсуждать вопросы удаления невидимых элементов изображения. Продемонстрируем только самый простой способ, применимый к изображениям многогранников. Назовём его "ручным" удалением элементов. С учётом положения исходной вершины и направления обхода эллипса установим индексы массивов, соответствующие рёбрам, а затем наложим условия на построение рёбер.
5030 IF NM<>2 AND NM<>3 AND NM<>4 THEN PLOT XL(NM),YL(NM) TO XL(NM+1),YL(NM+1) 5040 IF NM<>3 AND NM<>4 THEN PLOT XH(NM),YH(NM) TO XL(NM),YL(NM)
Аналогичным способом можно заменить сплошные изображения невидимых элементов на пунктирные, использовав при этом модифицированную подпрограмму "Отрезок".
Задание 2.6. Постройте изображение многогранника (рис.13), который мы будем называть n-угольным зубоскалом (он является частным случаем призматоида).
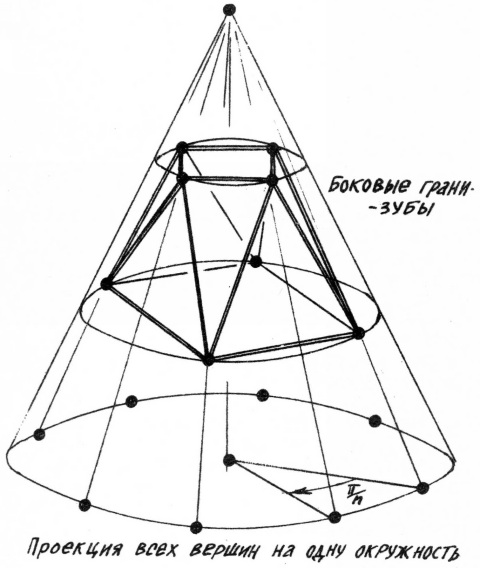
Решение. Зубоскал имеет 2*n вершин. Их положение в совокупности определяется углами, кратными π/n. В отличие от усечённой пирамиды, координаты вершин зубоскала не будем разбивать на две группы. Это позволит легко провести все рёбра: боковые - соединят соседние в массиве вершины, а лежащие в основании - через одну.
10 N=5 20 DIM X(2*N),Y(2*N): NM=0 30 R=50: R1=70: H=100: K=.5: X0=128: Y0=30 40 PI=4*ATN(1): A0=PI/6: S=l 50 A1=A0+2*PI 60 HOME I: PRINT "СЧЕТ" 70 GOSUB 2100 80 HGR=1: COLOR=15 90 GOSUB 5000 100 GET F¤: TEXT=0: END 2100 REM ЭЛЛИПС ......................................... 3100 REM ОБРАБОТКА КООРДИНАТ ЭЛЛИПСА 3110 X(NM)=XT: Y(NM)=YT 3120 NM=NM+1 3130 REM СМЕНА ОСНОВАНИЯ ЗУБОСКАЛА 3140 RR=R: R=R1: R1=RR 3150 Y0=Y0+S*H: S=-S 3160 RETURN 4100 REM ВЫБОР ШАГА 4110 DU=PI/N: RETURN 5000 REM ЗУБОСКАЛ 5010 FOR NM=0 TO 2*N-1 5020 PLOT X(NM),Y(NM) TO X(NM+1),Y(NM+1) 5030 PN=NM+2: IF PN>2*N THEN PN=1 5040 PLOT X(NM),Y(NM) TO X(PN),Y(PN) 5050 NEXT NM 5060 RETURN
Задание 2.7. Изменив предыдущую программу, постройте зубчатую звёздочку. Указание. Достаточно положить H=0, Y0=128, K=-5/3 и убрать строки 5030 и 5040.
Задание 2.8. Концы отрезка скользят по двум окружностям, лежащим в параллельных плоскостях. Постройте изображение поверхности, заметаемой отрезком (рис.14).
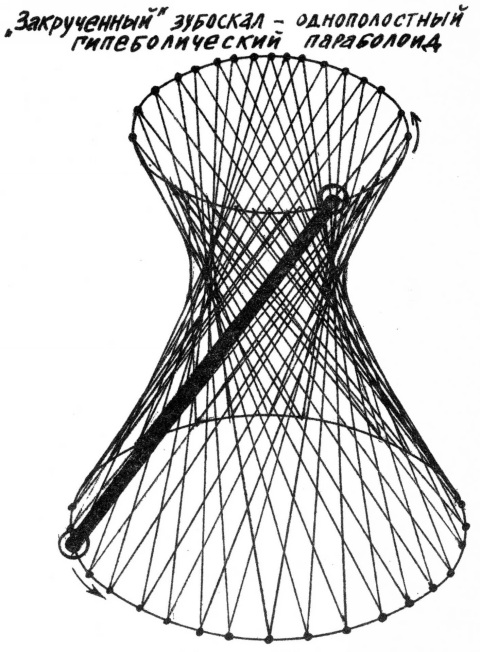
Решение. Используем программу из задания 2.7, удалив строки 5030 и 5040, а также заменив строки
10 N=32: M=19 50 A1=A0+2*M*PI 4110 DU=PI*M/N: RETURN
3. Построение изображений, связанных с шаром
Пять правильных многогранников (других не существует), изображённых на рисунках 15-19, называются Платоновыми телами, по имени философа Платона, который считал, что атомы четырёх элементов, признаваемых древними греками, имеют форму тетраэдра (огонь), октаэдра (воздух), икосаэдра (вода) и куба (земля), а Вселенная в целом имеет форму додекаэдра. С тех пор Платоновы тела прочно вошли в культуру человечества. Их рисовали Леонардо и Дюрер. Эта же задача стоит и перед нами.
3.1. Выбор оси вращения
Основным инструментом при построении Платоновых тел остаются круговые траектории, заметаемые вершинами многогранника при вращении вокруг некоторой оси. По понятным причинам, оси, не проходящие через центр описанного вокруг многогранника шара, следует сразу же отбросить. Таким образом для определения положения оси достаточно указать помимо центра шара ещё одну принадлежащую ей точку. После этого вершины разделятся на группы, каждая из которых принадлежит одной круговой траектории, образуемой сечением шара плоскостью, перпендикулярной оси и изображаемой на рисунке в виде эллипса. Рассмотрим три варианта выбора оси (рис.15-19).
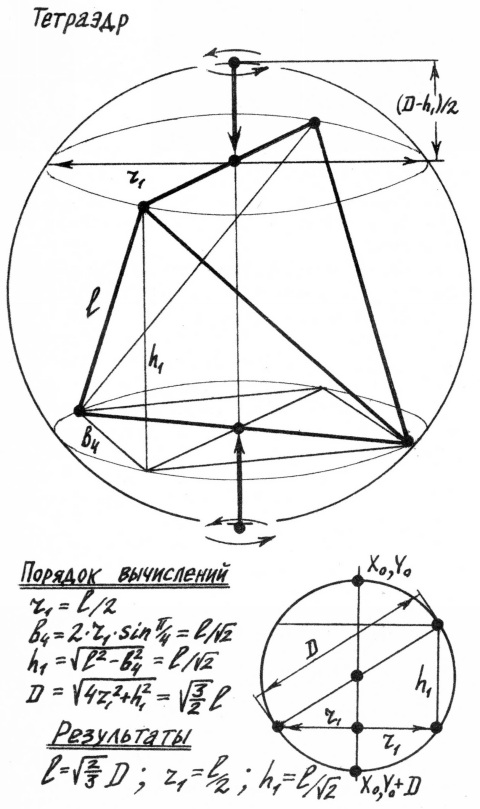
1. Ось проходит через середину ребра (тетраэдр).
2. Ось проходит через вершину (куб, икосаэдр).
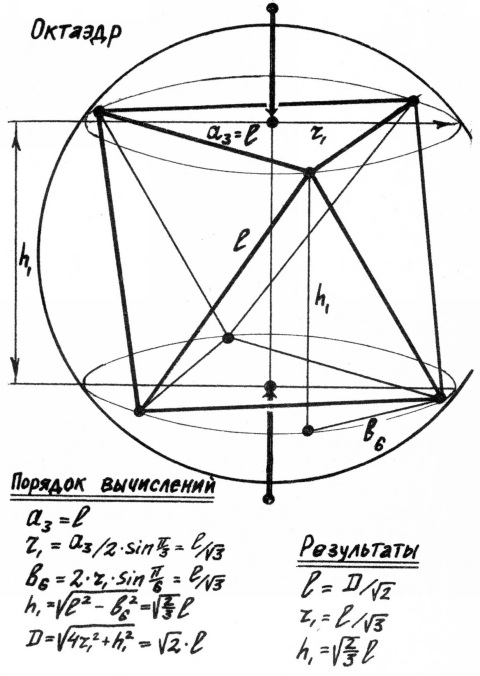
3. Ось проходит через центр грани (октаэдр, додекаэдр).
Обычно для куба выбирают третий вариант, а для тетраэдра и октаэдра - первый. Мы же остановились на более экзотическом их расположении.
Плоскости, в которых лежат траектории вершин, рассекают Платоновы тела на уже знакомые нам многогранники, открывая путь к построению нужных изображений.
1. Тетраэдр = двуугольный зубоскал (см. задание 2.6).
2. Октаэдр = треугольный зубоскал.
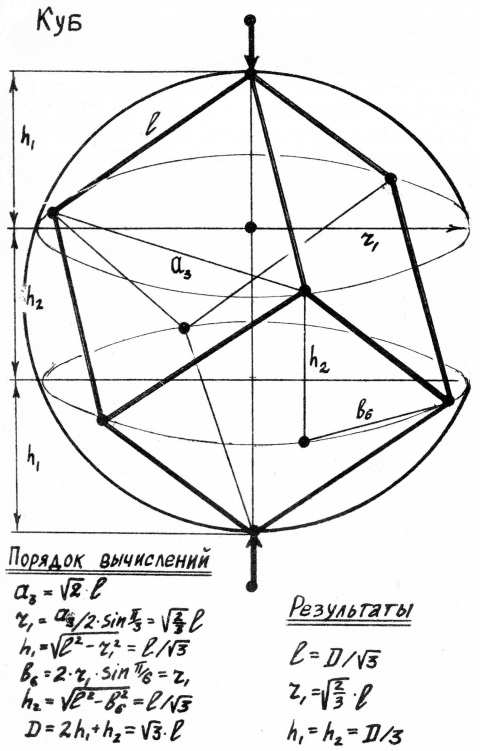
3. Куб = треугольный зубоскал +2 треугольных пирамиды.
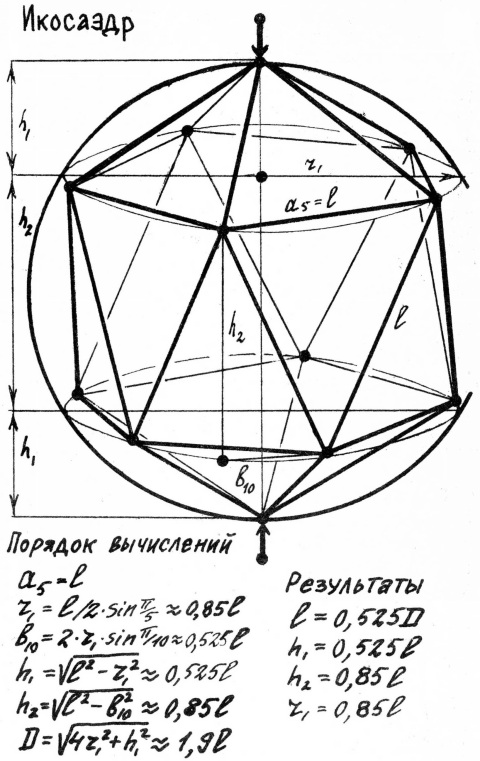
4. Икосаэдр = пятиугольный зубоскал +2 пятиугольных пирамиды.
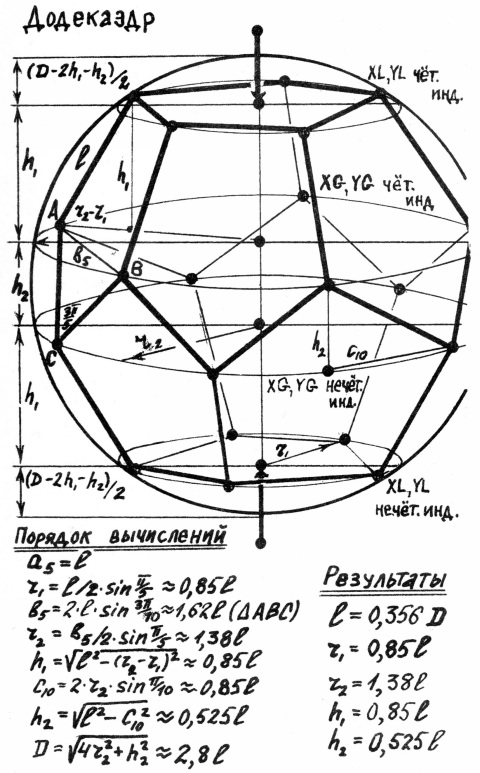
5. Додекаэдр = пятиугольный зубоскал +2 усечённых пятиугольных пирамиды.
3.2. Метрические соотношения для Платоновых тел
Высоты пирамид и зубоскалов, радиусы эллипсов не могут быть выбраны произвольно, так как внешний вид многогранника исказится. Нужно выразить все расстояния, характеризующие многогранник, через одну исходную величину. В качестве таковой мы возьмём диаметр описанного шара.
В процессе вычислений мы будем использовать известную формулу, выражающую зависимость между радиусом окружности и стороной вписанного в неё многоугольника:
an=2*r*sin π/n.
Все вычисления и их результаты приведены на рис.15-19.
Распишем порядок построения многогранников, общий для всех Платоновых тел.
1. Выбрать величины X0, Y0, D, задающие положение и длину вертикальной оси вращения.
2. Вычислить координаты центров эллипсов и их большие полуоси (радиусы).
3. Произвести вычисление и сохранение в массивах координат вершин многогранника. При этом следует учесть тот факт, что все вершины, лежащие выше центра шара, сдвинуты относительно вершин, лежащих ниже центра шара, подобно вершинам зубоскала.
Задание 3.3. Постройте изображения Платоновых тел.
Решение. В качестве примера продемонстрируем построение додекаэдра (без использования подпрограмм).
10 HGR=1: COLOR=15: PI==4*ATN(1) 20 X0=128: Y0=5: K=.25: I=0 30 D=180: A0=PI/4: DU=PI/5 40 L=D*.356: H1=L*.85: H2=L*.525 50 R1=L*.85*.6: R2=L*1.38*.6: REM К0ЭФ. 0.6 УЧИТЫВАЕТ СЖАТИЕ ЭКРАНА 60 Yl=Y0+(D-2*Hl-H2)/2 70 Y2=Y1+H1: Y3=Y2+H2: Y4=Y3+H1 80 DIM XL(10),YL(10),XG(10),YG(10) 90 FOR UG=A0 TO A0+2*PI+.1 STEP DU 100 XL(I)=X0+R1*COS(UG) 110 YL(I)=Y1-K*R1*SIN(UG) 120 YY=Yl: Yl=Y4: Y4=YY 130 XG(I)=X0+R2*COS(UG) 140 YG(I)=Y2-K*R2*SIN(UG) 150 YY=Y2: Y2=Y3: Y3=YY 160 I=I+l 170 NEXT UG 180 FOR I=0 TO 9 190 J=I+2: IF J>10 THEN J=J-10 200 IF I<>1 AND I<>9 THEN PLOT XL(I),YL(I) TO XL(J),YL(J) 210 IF I<>0 AND I<>1 AND I<>2 THEN PLOT XL(I),YL(I) TO XG(I),YG(I) 220 IF I=>3 AND I<=8 THEN PLOT XG(I),YG(I) TO XG(I+1),YG(I+1) 230 NEXT I 240 GET F¤: TEXT=0: END
Задание 3.4. Постройте изображение сферы, подчеркнув её форму меридианами и параллелями.
Решение. Заменим сферу вписанным в неё многогранником с большим количеством граней. Для этого разрежем её на слои горизонтальными плоскостями (рис.20). Каждый слой заменим правильной усечённой 2*n-угольной пирамидой. Боковые грани этих пирамид покроют поверхность сферы. Положение слоя определяется углом β, а положение грани в слое - углом α.
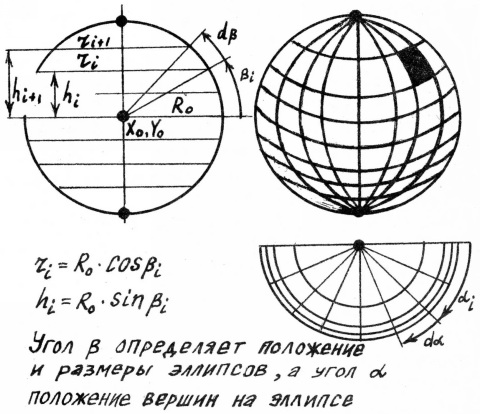
10 HGR=1: COLOR=15: PI=4*ATN(1) 20 X0=128: Y0=128: R0=120: K1=.6: K=-.5 30 N=18: DIM R(N),H(N),X1(N),Y1(N),X2(N),Y2(N1) 40 FOR I=0 TO N 50 R(I)=R0*K1*COS(-PI/2+I*РI/N) 60 H(I)=R0*SIN(-PI/2+I*PI/N) 70 NEXT I 80 FOR A=0 TO PI+.1 STEP PI/N 90 C=COS(A): S=SIN(A) 100 FOR I=0 TO N 110 X2(I)=X0+R(I)*C 120 Y2(I)=Y0+H(I)-R(I)*K*S 130 IF I=0 THEN PLOT X2(I),Y2(I) 140 IF I<>0 THEN PLOT TO X2(I),Y2(I) 150 NEXT I 160 FOR I=1 TO N-l 170 IF A=0 THEN 190 180 PLOT X1(I)=Y1(I) TO X2(I),Y2(I) 190 XI(I)=X2(I): Y1(I)=Y2(I) 200 NEXT I 210 NEXT A 220 GET F¤: TEXT=0: END
Литература
1. Бескин Н. M. Изображение пространственных фигур. - М.: Наука, 1971.