Навигационная цепочка "где я сейчас?" - траектория от главной до текущей страницы сайта. Breadcrumbs.
Передовица (меню разделов)
⇓
Документы
⇓
ИиО
⇓
Графические возможности диалоговой инструментально-учебной системы программирования
Графические возможности диалоговой инструментально-учебной системы программирования (N6/1991)
Машинная графика в рамках школьного курса ОИВТ представляет собой большой интерес. С одной стороны, как самостоятельный и очень важный раздел информатики, а с другой, как мощное педагогическое средство, позволяющее повышать наглядность обучения и его эффективность. Многолетний опыт проведения занятий со школьниками свидетельствует о том, что учащиеся, работая с машинной графикой, легче осваивают такие базовые понятия программирования, как циклы, ветвление, подпрограммы и т.п. [1]. Поэтому не случайно во всех современных учебных системах программирования присутствуют различные средства работы с машинной графикой.
Не является исключением в этом отношении и диалоговая инструментально-учебная система программирования (ДИУС) [2, 3, 4, 5]. Первые версии системы ДИУС были реализованы на ПЭВМ "Агат" седьмой модификации и написаны на языке Ассемблер микропроцессора 6502. Выбор данного компьютера обусловлен соображениями, изложенными в [6].
Апробация ДИУС проводилась в течение двух лет (1988-1989) в V-VI классах средней общеобразовательной школы. Контроль за физиологическим состоянием детей осуществлялся по программе, разработанной в НИИ ФДиП АПН СССР.
Входной язык системы, получивший название УМКА (Учебный микро-компьютерный алгоязык), обладает сравнительно небольшим набором команд (10), однако он является достаточно мощным языком программирования, позволяющим производить сложные математические расчёты, в полном объёме работать с символьной информацией, получать нетривиальные графические изображения, эффективно работать с динамической графикой, производить ввод и вывод алфавитно-цифровой информации, а также осуществлять музыкальный вывод.
Прежде чем говорить о графических возможностях системы ДИУС, представляется целесообразным проанализировать сначала, хотя бы вкратце, аналогичные возможности других учебных систем программирования. Учитывая всю сложность проведения такого анализа в пределах одной статьи, мы ограничимся лишь рассмотрением имеющихся подходов к организации графического вывода в указанных системах. При этом постараемся выяснить, с какими проблемами приходится сталкиваться школьнику, работающему в рамках того или иного подхода.
1. Машинная графика в декартовой и "черепашьей" системах координат.
Вообще говоря, графические возможности языка программирования зависят от того:
- в какой системе координат приходится оперировать пользователю, выводя на экран дисплея графическую информацию;
- каким набором графических примитивов (точка, отрезок, дуга и т.п.) он при этом располагает;
- какими дополнительными средствами обладает язык для манипулирования графической информацией (помимо традиционной возможности вывода графических примитивов).
Понятно, что среди перечисленных факторов ключевым является первый, т.е. используемая система координат. Именно она во многом определяет базовый набор примитивов и средства манипулирования графической информацией.
В учебных языках благодаря своей простоте наибольшее распространение получили декартовы и полярные координаты. При этом как в декартовой, так и в полярной системе координат точки могут задаваться либо абсолютными, либо относительными (относительно последней изображённой точки) значениями. Поэтому остановимся на четырёх возможных подходах.
Декартовы абсолютные координаты (ДАК) нашли своё воплощение в языках программирования BASIC, Рапира.
ДАК чрезвычайно удобны для построения графиков функций, однако для учебных систем программирования, ориентированных на школьников младших и средних классов, это свойство ДАК не представляется решающим.
Построение простейших рисунков в рамках ДАК осложняется необходимостью ссылаться на фиксированную точку отсчёта, которая нередко весьма удалена от самого рисунка. Помимо этого, ситуация часто усугубляется "перевёрнутостью" системы координат BASIC, сложностью работы с отдельными графическими примитивами. Например, для изображения дуги в рамках MSX-BASIC ребёнок должен указать семь параметров: координаты центра соответствующей окружности (задача нахождения этих координат для произвольной дуги является далеко не простой), начальный и конечный угол дуги "в радианах от направления направо против часовой стрелки" и т.д.
Возможности мультипликационного вывода на основе ДАК ограничены. С одной стороны, мультипликацию здесь программировать хлопотно из-за необходимости просчитывать на каждом шаге регенерации координаты всех ключевых точек объекта относительно центра, а с другой - расчёты, выполняемые интерпретатором, снижают скорость регенерации. Поэтому не случайно во многих BASIC-системах реализованы дополнительные средства графического вывода для получения качественной мультипликации (Sprite в MSX-BASIC, Shape в APPLESOFT-BASIC и т.п.), которые для привязки к ДАК требуют указания координат единственной точки.
Полярные относительные координаты (ПОК) нашли своё воплощение в языке программирования LOGO. Здесь ПОК удачно сочетаются с концепцией исполнителя (Черепашки).
Язык прост в изучении. С его помощью без труда можно построить квадрат, прямоугольник, равносторонний треугольник, а в цикле даже красивые многоугольные звёздочки. Однако попытка построить в рамках ПОК более "сложный" рисунок, например любой неравносторонний треугольник, неизбежно натолкнётся на проблему возврата в исходную точку (без теоремы синусов или косинусов здесь трудно обойтись). Авторы учебников по LOGO решают эту проблему либо за счёт использования в командах "НАПРАВО" и "НАЛЕВО" ограниченного набора угловых значений: 90°, 60° и 30° (sin 30° = cos 60° = 1/2), либо за счёт привлечения средств ДАК, а именно команд: "ДО xy" - передвинуть Черепашку до точки с координатами (x, y); "ДОАВСЦ x" и "ДООРД y" - передвинуть Черепашку горизонтально (вертикально) до точки с абсциссой x (ординатой y). Помимо этого, в рамках ПОК весьма непросто построить дугу и окружность. Для осуществления элементарного перемещения графического курсора ребёнку, работающему с LOGO, необходимо выполнить четыре команды: "ПОДНЯТЬ ПЕРО", "НАПРАВО", "ВПЕРЕД", "ОПУСТИТЬ ПЕРО".
Возможности мультипликационного вывода в рамках ПОК ограничены необходимостью вычислять на каждом шаге регенерации значения тригонометрических функций в каждой узловой точке объекта, а на это, как известно, требуется немало времени работы микропроцессора.
Однако необходимо признать, что педагогическая ценность учебной системы не может определяться одной лишь графикой. Простота и наглядность команд языка LOGO во многом окупают его графическую невыразительность.
Полярные абсолютные координаты (ПАК) ни в одном из известных учебных языков не нашли какого-либо логически завершённого воплощения. Во многих системах (LOGO, Школьница, ДИУС) графические команды на базе ПАК могут быть смоделированы, однако в качестве основы графического вывода они пока не используются, хотя и здесь вполне возможны интересные решения.
Декартовы относительные координаты (ДОК) легли в основу графики системы ДИУС.
Не секрет, что ДОК и раньше использовались в учебных языках программирования (BASIC, РАПИРА) для построения векторов, перемещения курсора, однако только в ДИУС ДОК были реализованы в "чистом" виде, т.е. на их основе строится вся графическая идеология языка УМКА (вывод примитивов, осуществление закраски, мультипликация, работа с фиксированными точками и т.п.).
ДОК обладают рядом очевидных достоинств.
Они просты в освоении, не требуют от ребёнка предварительных знаний об углах поворота, градусах, абсолютных координатах. Школьник должен лишь уметь находить величину смещения, переходя от одной точки на плоскости к другой.
ДОК позволяют осуществлять вывод всех графических примитивов в единообразной форме, благодаря чему графика ДИУС базируется практически на одной команде. В связи с этим ребёнку одинаково просто нарисовать на экране точку, отрезок, дугу, окружность.
В рамках ДОК удобно строить рисунки произвольной сложности, так как, с одной стороны, отсчёт всегда ведётся от текущей точки, которая всегда "под рукой", а с другой стороны, с помощью дуг легко аппроксимируются любые кривые.
ДОК позволяют достаточно просто получать качественную мультипликацию. Во-первых, она без труда программируется, не требуя от ребёнка использования команды присваивания. Во-вторых, регенерация изображения осуществляется практически моментально, так как микропроцессор оперирует исключительно с целыми константами на уровне машинных команд ADC (сложить) и SBC (вычесть).
Среди недостатков ДОК можно отметить общую для всех относительных координат проблему возврата в исходную точку. Однако в рамках ДИУС эта проблема решается достаточно просто с помощью механизма фиксированных точек, который описывается ниже.
2. Машинная графика на основе одной команды.
'РИС' - единственная команда языка УМКА, обеспечивающая вывод графической информации. Формат команды следующий: РИС код операции, ΔX, ΔY.
Здесь "код операции" - это символ, указывающий на характер выполняемого действия (например, '/' - построить отрезок, - осуществить закраску и т.п.); 'ΔX, ΔY' - смещение относительно текущей точки. Положительный отсчёт координат по оси X ведётся слева направо, а по оси Y снизу-вверх.
Итак, команда 'РИС' позволяет:
изменять позицию графического курсора, т.е. осуществлять перескок от текущей точки к точке, смещение до которой указано в команде, например: РИС^,10,20
изображать отрезок от текущей точки к точке, смещение до которой указано в команде, например: РИС/,200,0
изображать дугу от текущей точки к точке, смещение до которой указано в команде, например:
РИС (,20,30 - малая левая дуга (рис. 1,b); РИС ),20,30 - малая правая дуга (рис. 1,c); РИС [,20,30 - большая левая дуга (рис. 1,a); РИС ],20,30 - большая правая дуга (рис. 1,d).
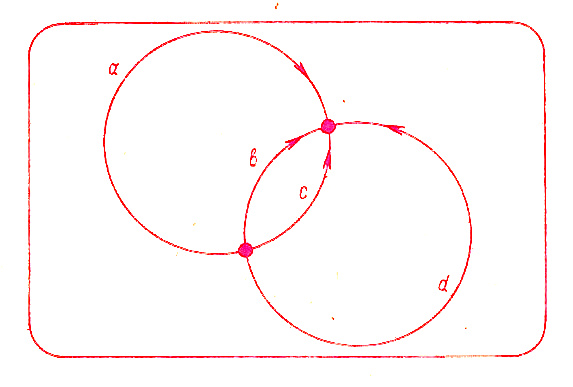
После запуска системы автоматически устанавливается значение радиуса, равное 30. Для того чтобы задать новое значение радиуса, необходимо его числовое представление записать перед кодом дуги. Например: РИС 10[,20,20
Изображать окружность. Для этого необходимо построить большую дугу с минимальным смещением (0,1), (1,1) и т.п. в зависимости от требуемой ориентации окружности. Например: РИС [,0,1 РИС],1,1 РИС [,1,0
Производить закраску замкнутой области. В данном случае смещение будет определять точку, начиная с которой необходимо осуществлять закрашивание. Например: РИС #,1,1
Изменять цвет выводимой графической информации. При запуске ДИУС автоматически устанавливается белый цвет вывода. Для изменения цвета необходимо в одной из трёх команд: 'перескок', 'отрезок', 'закраска' - перед кодом команды записать код цвета. Например: РИС^0,0,0 РИС 1#2,2
Фиксировать положение текущей точки в стеке. Данная возможность бывает полезной при изображении сложных рисунков. Как правило, в этом случае возникает необходимость вернуться к точкам, которые уже были использованы в процессе изображения. Поэтому, реализуя настоящую возможность, пользователь может запоминать в стеке положение узловых точек рисунка с тем, чтобы впоследствии иметь возможность вернуться к ним без подсчёта соответствующего смещения. Для однократного фиксирования положения текущей точки в стеке используется команда 'РИС' без параметров: РИС. Для многократного фиксирования положения текущей точки в стеке после ключевого слова 'РИС' указывается соответствующее количество запятых. Например, команда РИС ,,, осуществляет четырёхкратное фиксирование положения текущей точки в стеке;
Осуществлять возврат к ранее зафиксированным в стеке точкам. Возврат может быть реализован в виде перескока, проведения отрезка, дуги и т.п. Для осуществления возврата необходимо в команде 'РИС' опустить смещение. Например: РИС/
Провести отрезок от текущей точки до точки, положение которой зафиксировано на вершине стека. После использования зафиксированной на вершине стека точки информация о ней из стека выталкивается и для работы становится доступной точка, которая была зафиксирована в стеке ранее;
Комбинировать все перечисленные выше возможности в рамках одной команды. Например: РИС^,20,100,/,20,-100,/,20,100 РИС ,/,10,20,/,10,-40,/
Отменять результат выполнения последней команды 'РИС'. Данная возможность полезна в двух случаях: во-первых, для исправления неверно выполненных действий при работе в диалоговом режиме и, во-вторых, для организации мультипликационных изображений в программном режиме. В первом случае отмена осуществляется без смещения, т.е. с возвратом к предыдущей текущей точке. Команда имеет вид: РИС -
Во втором же случае для обеспечения динамики необходимо изменять положение текущей точки на величину смещения. Команда имеет вид: РИС -,5,2 Пример программы, осуществляющей простейшую мультипликацию:
ПОВТОР 40
▄─────────────────────────────────▄
РИС /,20,0,/,-5,5,/,-10,0,/,-5,-5
РИС -,3,2
▄_________________________________▄
Здесь первая команда 'РИС' осуществляет изображение летающей тарелки. Команда 'РИС -, 3,2' осуществляет ликвидацию полученного изображения с последующим смещением графического курсора. Многократный повтор этой группы команд позволяет получить на экране эффект мультипликационного изображения. Варьируя величину смещения в отменяющей команде 'РИС', можно изменять направление движения объекта и его скорость.
Порядок построения простейших рисунков с помощью команды 'РИС' продемонстрируем на следующем примере. Допустим, мы хотим получить на экране дисплея изображение Микки Мауса (рис.2).

Для этого мы должны в первую очередь выделить на рисунке основные узловые точки, т.е. точки, которые разбивают линии изображения на фрагменты, близкие к дугам и отрезкам (рис.3).
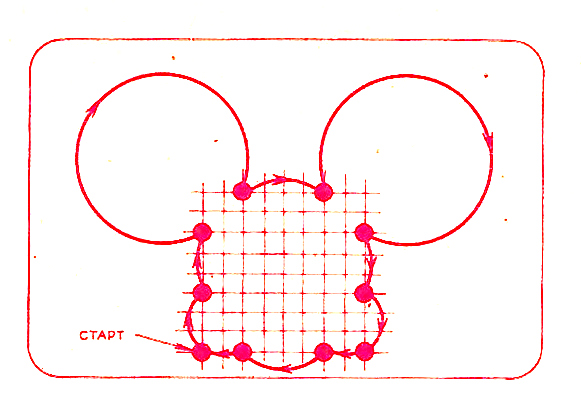
Затем, учитывая смещения, соединяем узловые точки соответствующими дугами и отрезками:
РИС (,0,30, (, 0, 30 РИС [,20,20, (, 40, 0, , 20,-20 РИС (,0,-30, (, 0,-30 РИС §,-20,0, (,-40, 0, /,-20, 0
В результате мы получим "каркас" нашего изображения, обрисованный дугами одного радиуса. Осталось подобрать подходящие значения радиусов для каждой дуги с тем, чтобы приблизить "каркас" к желаемому виду:
РИС 16(, 0, 30, 40(, 0, 30 РИС (, 20, 20, (, 40, 0, [, 20,-20 РИС (, 0,-30, 16(, 0,-30 РИС /,-20, 0, 25(,-40, 0, /,-20, 0
Помимо простых рисунков система ДИУС позволяет получать и более "серьёзные" изображения: графики функций, круговые диаграммы, проекции тел трёхмерного пространства и многое другое [4]. Например, следующая программа строит гистограмму на основе значений, генерируемых датчиком случайных чисел (рис.4).

ПОВТОР 10
▄─────────────────────────────────▄
РИС
ПОВТОР INT(100*RND(1))
▄───────────────────────────────▄
РИС /,20,0,^,-20,1
▄_______________________________▄
РИС ^,^,20,0
▄_________________________________▄
Если же рамки команды 'РИС' тесны для пользователя, то он всегда может смоделировать в рамках ДИУС необходимую ему графическую среду, которая наиболее полно отвечала бы его потребностям.
3. Создание других графических команд в системе ДИУС.
В отличие от существующих учебных систем программирования ДИУС обладает уникальными инструментальными свойствами, благодаря чему преподаватель имеет возможность приспосабливать учебную среду к своим нуждам, подчинять входной язык собственной методической схеме. В рамках системы могут быть видоизменены команды входного языка, смоделированы операторы и конструкции известных учебных языков программирования, реализованы новые экспериментальные языки и многое другое.
Механизм порождения и использования новых команд весьма прост и не выходит за рамки правил работы с обычными подпрограммами языка УМКА, поэтому даже ребёнок может придумывать и создавать свои собственные команды. Как показал опыт, дети с большим интересом воспринимают данную возможность.
Не вдаваясь в подробности, отметим, что инструментальные возможности ДИУС обеспечиваются наличием в системе:
- специальной области памяти, предназначенной для хранения подпрограмм (написанных на языке УМКА), благодаря чему преподаватель может "прятать" от ребёнка вновь определённые операторы;
- инструментального режима работы, позволяющего осуществлять редактирование подпрограмм, хранящихся в указанной области памяти;
- самим порядком организации работы с подпрограммами, причём вызов вновь определённых команд синтаксически не отличается от обращения к встроенным командам входного языка.
Итак, на основе десяти встроенных команд входного языка и механизма создания новых команд преподаватель, например, может смоделировать графические команды таких учебных языков, как
MSX-BASIC LINE (10,10)-(10,200),1
LINE (10,200)-(150,150),1
LINE (150,150) -(10,10),1
PAINT (100,100),1
APPLESOFT-BASIC COLOR=1
PLOT 10,10
PLOT TO 10,200
PLOT TO 150,150
PLOT TO 10,10
LOGO ЦЕНТР
БЕЗСЛЕДА
ВЛЕВО 60
ВПЕРЕД 30
РАПИРА: ТРЕУГОЛЬНИК (10,10,10,200,150,150)
ПРЯМОУГОЛЬНИК (0,0,80,60)
ЛИНИЯ (0,0,100,100)
с тем, чтобы работать с новыми командами как со встроенными командами входного языка.
В заключение отметим, что простота освоения системы и небольшой набор команд входного языка позволяют использовать ДИУС для обучения школьников младших, средних и старших классов, а также система может оказаться полезной для любого пользователя, начинающего изучать информатику. Как показала апробация, система способна существенно облегчить процесс формирования у обучаемых основных понятий и навыков программирования. Дети буквально с первого урока начинают практическую работу на компьютере, быстро осваивают команды входного языка, без затруднений переходят к другим языкам и системам программирования.
Для получения дополнительной информации о системе ДИУС необходимо написать по адресу: 637002, Павлодар, ул.Мира, 60, Павлодарский пединститут, кафедра информатики; тел.: 75-29-95.
- Литература
- Звенигородский Г.А., Салихова А.К., Цикоза В.А. Машинная графика в математическом обеспечении учебного процесса // Прикладные методы информатики. Новосибирск, 1980.
- Беркуцкий В.Я., Поливаный И.В. Диалоговая инструментально-учебная система программирования // Микропроцессорные средства и системы. 1990. N1. c.35.
- Поливаный И.В. Диалоговая инструментально-учебная система программирования: Руководство пользователя. Павлодар, 1991.
- Беркуцкий В.Я., Поливаный И.В. Диалоговая инструментально-учебная система программирования: Пособие для учителя. Павлодар, 1991.
- Поливаный И.В. Диалоговая система программирования начального обучения (ДИУС) // Актуальные вопросы педагогической технологии качества учебного процесса. Труды региональной межвузовской научно-методической конференции. Алма-Ата, 1990.
- Беркуцкий В.Я., Поливаный И.В., Щеглов С.А. Лица "Агата" // Информатика и образование. 1989. N5. с.71-72.